첫 과제 구현 정리
문제
장애물 4개가 있는 8x8 체스판에 8개의 Queen을 서로 공격할 수 없도록 배치한다.
제약사항
1. 메인 함수 및 함수 입력 조건은 수정하지 않음.
2. 프로그램 예시 결과 화면에서 나타나는 출력 형식과 동일하게 출력.
3. 6가지 함수를 사용.
void setBoard();
void printBoard();
void setBlockedPositions();
int isBlocked(int row, int col);
int isSafe(int row, int col);
int solveNQueens(int row);
함수 기능
1. void setBoard();
보드의 크기에 맞는 행렬을 생성하여 반환.
행렬의 각 성분은 0으로 기본 초기화.
2. void printBoard();
최종 배치된 보드의 형태 및 모든 성분을 출력.
3. void setBlockedPositions();
퀸이 놓일 수 없는 4개의 랜덤한 자리를 선택하여 -1로 설정.
blocked 배열을 통해 선택된 위치를 저장하고, 해당 자리를 체스판에서 표시.
4. int isBlocked(int row, int col);
주어진 자리가 blocked 위치인지 확인.
blocked 위치인 경우 1을 반환하고, 그렇지 않으면 0 반환.
5. int isSafe(int row, int col);
현재 위치에 퀸을 놓을 수 있는지 확인.
같은 열, 왼쪽 대각선, 오른쪽 대각선에 퀸이 있는지와 Blocked 위치인지 확인.
놓을 수 없으면 0(False), 놓을 수 있으면 1(True) 반환.
6. int solveNQueens(int row);
퀸을 체스판에 배치 행을 하나씩 내려가며 재귀적으로 배치가 가능한 열을 확인.
구현과정
main 함수
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 8
int board[N][N];
int blocked[4][2]; // 퀸이 위치할 수 없는 랜덤한 4개의 자리
void setBoard();
void printBoard();
void setBlockedPositions();
int isBlocked(int row, int col);
int isSafe(int row, int col);
int solveNQueens(int row);
int main(void)
{ // main 변경 x
srand(time(NULL)); // 랜덤 넘버 생성기 초기화
setBoard(); // N x N 체스판, 0으로 초기화 (빈칸)
setBlockedPositions(); // 랜덤한 4개의 blocked 자리 설정
if (solveNQueens(0))
{
printBoard(); // 성공하면 퀸의 배치를 출력
}
else
{
printf("Solution does not exist\n");
}
return 0;
}1. setBoard 구현
// 체스판을 0으로 초기화
void setBoard()
{
// 과제1. 구현(1) setBoard 함수 구현하기
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
board[i][j] = 0;
}board 배열을 선언할 때 0으로 초기화하지 않고, setBoard 함수를 통해 초기화하는 것이 다소 불필요해 보였지만 과제의 요구사항이므로 그대로 구현하였다.
이 코드에서 주목할 만한 점은 2차원 배열의 순회 방식이다. setBoard 함수는 행(row)을 기준으로 배열을 순회하고 있다. 대부분의 경우 이중 for문 작성 시 이처럼 행을 기준으로 순회하도록 하는 것이 일반적이다. 그러나 이는 사실 data locality를 고려한 접근 방식으로 메모리 효율성을 높이기 위한 방법이다.
2차원 배열은 사실상 1차원 배열들의 집합으로 메모리에 할당된다. 2차원 배열은 행 단위로 메모리에 연속적으로 저장되기 때문에, 행을 기준으로 순회하면 연속된 메모리 주소에 접근하여 cache hit rate가 높아진다. 반면, 열을 기준으로 순회하면 연속된 메모리 주소에 접근하지 않기 때문에 cache hit rate이 낮아져 상대적으로 느린 메모리 접근을 유발한다.
이중 for문 작성 시 당연하게 2차원 배열을 순회할 때는 행(row)을 기준으로 순회하도록 코드를 작성해왔다. 위 내용은 시스템 프로그래밍 수업에서 다룬 내용인데, 이런 점을 주목하고 분석해보는 재미가 있는 것 같다.
2. setBlockPositions 구현
초기에는 다음의 두 가지 방법으로 setBlockedPositions 함수를 구현하였다.
// 랜덤한 4개의 자리를 blocked 위치로 설정
void setBlockedPositions()
{
// 과제1. 구현(2) setBlockedPositions 함수 구현하기
for (int i = 0; i < 4; i++)
{
int x = rand() % 8;
int y = rand() % 8;
blocked[i][0] = x;
blocked[i][1] = y;
board[x][y] = -1;
}
}// 랜덤한 4개의 자리를 blocked 위치로 설정
void setBlockedPositions()
{
// 과제1. 구현(2) setBlockedPositions 함수 구현하기
for (int i = 0; i < 4; i++)
{
for(int j=0; j<2; j++){
int coordinate = rand() % 8;
blocked[i][j]=coordinate;
}
board[blocked[i][0]][blocked[i][1]]=-1;
}
}첫 번째 구현에서는 행(x)과 열(y) 좌표를 각각 생성하여 blocked 배열과 board 배열에 저장하였다. 반면, 두 번째 구현에서는 이중 for 문을 사용하여 blocked 배열에 좌표를 저장한 후, board 배열에서 해당 좌표에 –1을 대입한다.
두 코드 모두 시간 복잡도가 O(1)로 동일하고, 연산 시간에도 큰 차이가 없으나 첫 번째 구현 방식이 가독성 더 가독성이 뛰어나다. 또한 동일한 좌표가 생성되는 경우를 방지하기 위해 좌표 중복 여부를 체크하는 로직을 추가할 필요가 있었는데, 두 번째 구현은 이중 for문을 사용하여 좌표를 저장한 후 새로운 난수를 생성하므로, 중복 여부를 확인하고 처리하는 데 어려움이 있었다.
따라서 중복된 좌표 생성 문제를 방지하고 코드의 가독성을 높이기 위해, 첫 번째 구현 방식을 사용하는 것이 더 적합하다고 판단하였다. 최종적으로 첫 번째 방식을 기반으로 중복 처리 로직을 포함해 구현을 완료하였다.
// 랜덤한 4개의 자리를 blocked 위치로 설정
void setBlockedPositions()
{
// 과제1. 구현(2) setBlockedPositions 함수 구현하기
int cnt = 0;
while (cnt < 4)
{
int x = rand() % N; // 0 ~ N-1의 랜덤한 정수 생성
int y = rand() % N; // 0 ~ N-1의 랜덤한 정수 생성
if (board[x][y] != -1) // 이전에 생성된 좌표인지 확인
{
blocked[cnt][0] = x;
blocked[cnt][1] = y;
board[x][y] = -1; // board에 장애물 추가
cnt++;
}
}
}board size가 매크로 상수 N에 의해 정의되므로 N으로 수정해주었다. 4개의 장애물 좌표를 생성할 때까지 while 루프를 실행한다. 이때 변수 cnt를 이용해 새로 생성된 좌표일 경우만 카운트하여 반복하도록 설정했다.
3. printBoard 구현
// 체스판 출력 함수
void printBoard()
{
// 과제1. 구현(3) printBoard 함수 구현하기
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
switch (board[i][j])
{
case -1:
printf("X ");
break;
case 0:
printf(". ");
break;
case 1:
printf("Q ");
break;
default:
printf("?");
break;
}
}
printf("\n");
}
}특별한 로직은 없다. board 배열의 값을 기반으로 “X ”, “. ”, “Q ” 3가지를 출력해야 하기 때문에 switch문을 이용했다. switch 문은 여러 값에 대한 조건 분기를 간결하게 처리할 수 있기 때문에 if-else 문보다 가독성이 좋다. 이 코드에서는 for문을 사용해 board 배열을 순회하며 값에 따라 “X ”, “. ”, “Q ” 를 출력해야 하므로, switch 문을 사용하는 것이 적절하다.
에러 발생 시 board 배열에 예상하지 못한 값이 존재할 수 있으므로 default 케이스로 "? "를 출력하도록 구현하였다.
4. isBlocked 구현
// 해당 자리가 blocked 위치인지 확인
int isBlocked(int row, int col)
{
// 과제1. 구현(4) isBlocked 함수 구현하기
if (board[row][col] == -1) // blocked이면 1 반환
return 1;
return 0; // blocked 아니면 0 반환
}주어진 위치가 장애물로 설정된 위치인지 확인한다. board[row][col]의 값이 –1이면 1을, 아니면 0를 반환한다.
5. isSafe 구현
// 현재 위치에 퀸을 놓을 수 있는지 확인
int isSafe(int row, int col)
{
// 과제1. 구현(5) isSafe 함수 구현하기
if (isBlocked(row, col)) // 장애물이 있는지 확인
return 0;
for (int i = 0; i < row; i++) // 이전 행 검사
{
if (board[i][col] == 1) // 같은 열에 퀸이 있는지 확인
return 0;
int c = row - i; // 기준 상수
if (col + c < N && board[i][col + c] == 1) // 우상향 대각선에 퀸이 위치하는지 확인
return 0;
if (col - c >= 0 && board[i][col - c] == 1) // 좌상향 대각선에 퀸이 위치하는지 확인
return 0;
}
return 1; // safe
}isSafe 함수는 주어진 위치에 퀸을 배치할 수 있는지 확인한다. 우선 주어진 위치가 장애물인지 여부를 확인한다. isBlcoked 함수를 호출해 장애물이 존재(1을 반환)하면 0을 반환하고 함수를 종료한다. 장애물이 존재하지 않는다면 같은 열에 퀸이 존재하는지 확인한다.
row 이전의 모든 행을 순회하여 board[i][col]이 1, 즉 같은 열에 퀸이 존재한다면 0을 반환하고 함수를 종료한다. 그렇지 않다면 대각선에 퀸이 존재하는지를 검사한다.
대각선 검사는 row 이전의 모든 행을 순회하며, 우상향 대각선과 좌상향 대각선을 확인한다. row – I의 값을 c로 정의한다. col + c가 N보다 작고, board[i][col + c]이 1이면 우상향 대각선에 퀸이 존재하는 것으로 0을 반환한다. col – c가 0 이상이고 board[i][col – c]가 1이면 좌상향 대각선에 퀸이 존재하는 것으로 0을 반환한다. 모든 조건을 통과하면 1을 반환해 퀸을 놓을 수 있음을 알린다.
이 코드는 3가지 조건을 차례로 검사한다. return이 호출되면 함수는 종료되므로 나머지 판단을 생략할 수 있기 때문에 효율성을 고려하여 가장 간단한 조건부터 검사하도록 구성하였다.
문제가 되었던 부분은 대각선 판단 로직이다. 초기에는 이중 for문을 이용해 모든 좌표를 순회하고, (row, col)과의 기울기를 비교하여 대각선 여부를 판단하려 했다. 하지만 모든 좌표를 검사해야 하기 때문에 연산 시간이 길어지고 비효율적이라는 생각이 들었다. 이를 개선하기 위해 아래와 같이 행을 하나씩 순회하면서, 대각선에 위치하는 좌표만을 검사하는 알고리즘을 고안하였다.
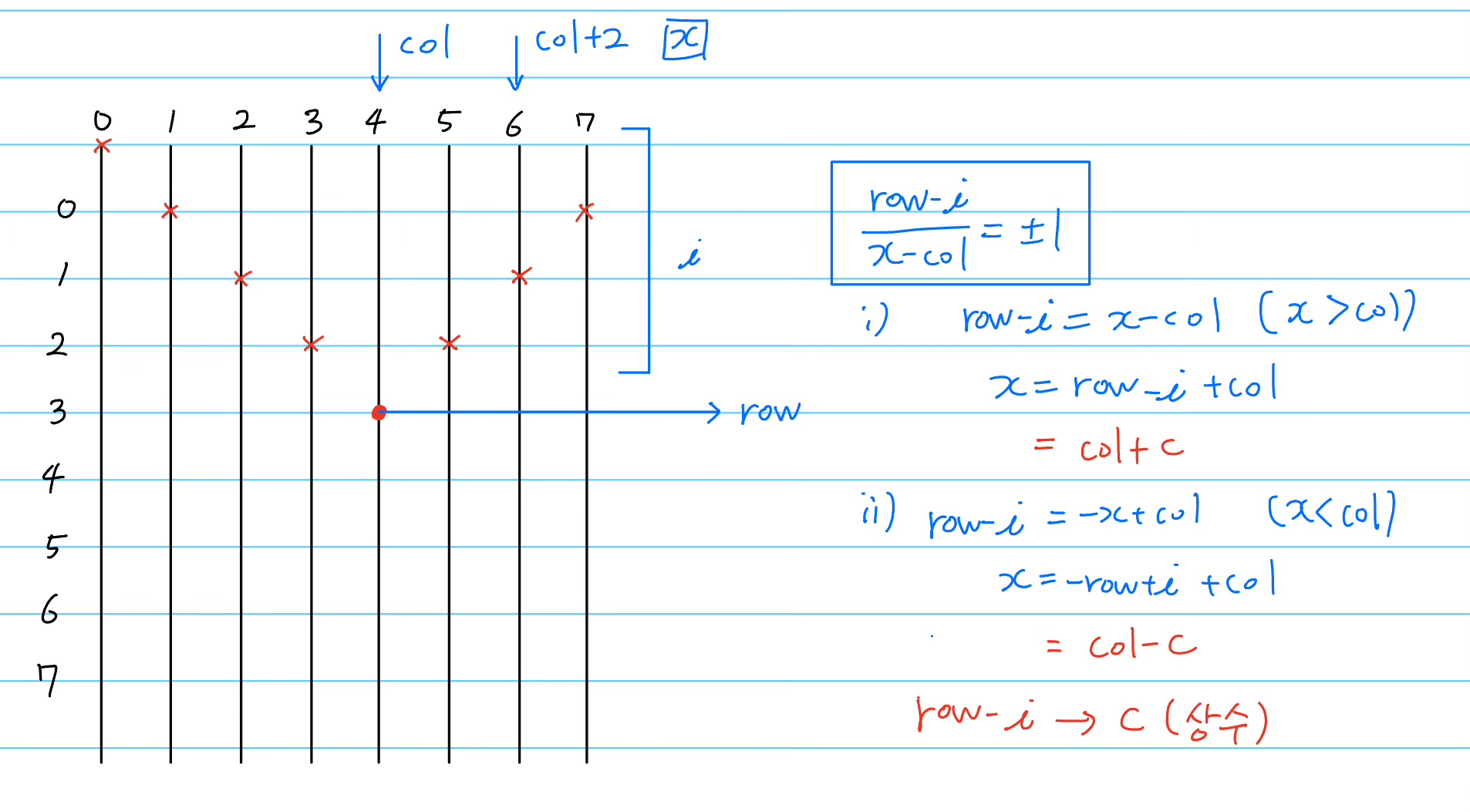
행을 하나씩 순회하므로, i번째 행을 검사할 때 대각선에 위치하는 좌표만을 검사하도록 하면 모든 좌표를 검사할 필요가 없어진다. 위 이미지에서 현재 좌표를 (row, col) = (3, 4)로 가정하고 구상해보았다. 검사해야 할 좌표를 (i, x)로 가정한다. 이때 x는 현재 열인 col열을 기준으로 달라진다. (row, col)과 (i, x)의 기울기를 판정하려면 다음과 같은 식을 작성할 수 있다.
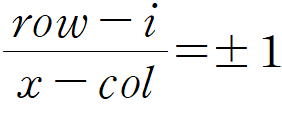
그리고 위 식에서 x와 col의 대소관계에 따라 범위가 달라지게 된다.


i)는 우상향 대각선을, ii)는 좌상향 대각선을 판단할 때 열을 나타낸다. i번째 행마다 x가 결정되므로 대각선 좌표만을 추출할 수 있게 되었다. 이를 이용해 x값을 결정하고, board[i][x]에 퀸이 존재하는지를 판단하면 된다. 다만 x는 0~7의 값이어야 하므로 범위 설정이 필요하다.
두 식에서 공통적으로 나타나는 row - i를 c라는 상수로 정의하였다. 그 결과 우상향 대각선 판정에서 x = col + c가 되고 좌상향 대각선 판정시에는 x = col - c가 된다. 우상향 대각선은 col의 오른쪽 열을 검사하므로 col + c는 7보다 커서는 안된다. 즉, col = c < N이어야 한다. 좌상향 대각선은 col의 왼쪽 열을 검사하므로 col - c는 0보다 작아서는 안된다. 즉, col - c >= 0이어야 한다.
이를 기준으로 위 코드와 같이 대각선 판단 로직을 구현하였으며, 모든 조건을 통과하면 1을 반환하도록 하였다.
6. solveNQueens 구현
solveNQueens는 행을 하나씩 내려가며 재귀적으로 배치가 가능한 열을 확인하고 퀸을 배치한다. solveNQueens 함수의 동작을 정리하면 다음과 같다.
1. row행의 모든 열을 순회하여 퀸을 놓을 수 있는지 확인한다.
2. 퀸을 놓을 수 있는 열이라면 퀸을 배치한다.
3. 종료 조건으로 row가 N-1보다 크면 1을 반환한다.
위 동작을 recursion 함수로 구현하면 다음과 같다.
// 퀸을 체스판에 배치하는 재귀 함수
int solveNQueens(int row)
{
// 과제1. 구현(6) solveNQueens 함수 구현하기
if (row > N - 1) // 모든 행에서 수행 완료
return 1;
for (int i = 0; i < N; i++)
if (isSafe(row, i)) { // 해당 좌표에 퀸을 놓을 수 있는지 확인
board[row][i] = 1;
break;
}
solveNQieens(row+1); // 다음행 검사
}그러나 이 구현에서는 몇가지 문제가 있었다. solveNQueens(row + 1)의 반환값을 확인하지 않기 때문에 이후 행에서 해를 찾지 못하더라도 계속해서 퀸을 배치한다.
따라서 잘못된 배치로 인해 전체적인 해결이 불가능해진다. 만약 다음 행에서 퀸을 배치할 수 없다면 이전에 배치된 퀸을 제거하고 다시 시도하는 백트래킹이 필요하다.
하지만 초기 구현에는 이러한 처리 로직이 없어 문제가 발생했다. 마지막으로, solveNQueens 함수의 반환값을 제대로 처리하지 않기 때문에, 마지막 재귀 호출을 제외한 나머지 재귀 호출의 반환값이 존재하지 않아 문제가 발생했다.
이 문제를 해결하기 위해 백트래킹을 구현하고, 재귀 호출의 반환값을 확인하여 해를 찾지 못한 경우 이전에 배치한 퀸을 제거하도록 개선하였다.
// 퀸을 체스판에 배치하는 재귀 함수
int solveNQueens(int row)
{
// 과제1. 구현(6) solveNQueens 함수 구현하기
if (row > N - 1) // 모든 행에서 수행 완료
return 1;
for (int i = 0; i < N; i++)
{
if (isSafe(row, i)) // 해당 좌표에 퀸을 놓을 수 있는지 확인
{
board[row][i] = 1;
if (solveNQueens(row + 1)) // 다음 행에서 recursion
return 1;
board[row][i] = 0; // 다음행에서 해를 찾지 못했으므로 되돌림
}
}
return 0;
}현재 행에서 각 열을 순회해 퀸을 배치할 수 있는 지 isSafe 함수를 통해 확인한다. 퀸을 배치할 수 있는 경우, 해당 위치에 퀸을 배치한 후 다음 행에 대해 재귀 호출 solveNQueens(row + 1)을 수행한다. 해를 발견하면 solveNQueens(row + 1)가 1을 반환하고, 최종적으로 모든 퀸을 배치하는 해를 찾으면 1을 반환하여 함수를 종료한다. 해를 찾지 못한 경우에는 현재 위치에 놓인 퀸을 제거하고 다음 열로 이동하는 백트래킹을 수행한다. 모든 열을 검사했으나 퀸을 배치할 수 있는 해를 찾지 못하면 0을 반환한다.
하지만 recursion 함수의 특성 상 함수의 흐름 이해가 쉽지 않다. recursion 시 마다 스택 프레임이 생성되고, 해당 함수의 매개변수, 지역 변수, 반환 주소 등이 이 프레임에 저장된 후 스택에 푸시(push)된다. 스택은 LIFO(Last In, First Out) 구조이므로, 마지막에 호출된 함수가 먼저 종료되면 해당 스택 프레임이 팝(pop)되어 스택에서 제거된다.
즉, solveNQueens(row + 1)의 호출 시 마다 이전 스택프레임은 대기 상태로 스택에 유지되고, 다음 recursion이 종료 된 이후 이전 함수가 다시 실행된다.
이러한 구조로 인해 solveNQueens(0) 호출 시 다음과 같은 구조로 수행된다.
solveNQueens(0)
├── 퀸 배치: row=0, col=0
├── 다음 재귀 호출: solveNQueens(1)
├── 퀸 배치: row=1, col=4
├── 다음 재귀 호출: solveNQueens(2)
├── 퀸 배치: row=2, col=5 => 백트래킹 발생, return 0 (첫 번째 백트래킹)
├── solveNQueens(2) (백트래킹 후 다른 열 시도)
├── 퀸 배치: row=2, col=7
├── 다음 재귀 호출: solveNQueens(3)
├── 퀸 배치: row=3, col=4 => 백트래킹 발생, return 0 (두 번째 백트래킹)
├── solveNQueens(3) (백트래킹 후 다른 열 시도)
├── 퀸 배치: row=3, col=5
├── 다음 재귀 호출: solveNQueens(4)
├── 퀸 배치: row=4, col=6 => 백트래킹 발생, return 0 (세 번째 백트래킹)
├── solveNQueens(4) (백트래킹 후 다른 열 시도)
├── 퀸 배치: row=4, col=2
├── 다음 재귀 호출: solveNQueens(5)
├── 퀸 배치: row=5, col=6
├── 다음 재귀 호출: solveNQueens(6)
├── 퀸 배치: row=6, col=1
├── 다음 재귀 호출: solveNQueens(7)
├── 퀸 배치: row=7, col=3
├── solveNQueens(8) => 모든 퀸 배치 완료, return 1
└── solveNQueens(7) => return 1
└── solveNQueens(6) => return 1
└── solveNQueens(5) => return 1
└── solveNQueens(4) => return 1
└── solveNQueens(3) => return 1
└── solveNQueens(2) => return 1
└── solveNQueens(1) => return 1
└── solveNQueens(0) => return 1
'Data Structure & Algorithm' 카테고리의 다른 글
| [자료구조및알고리즘이해] 원형 Queue (0) | 2024.11.13 |
|---|
